Vectors Calaulus 1.17

PROBLEM 5  

Find the parametric equations of the tangent line to the curve that is formed by intersecting the sphere  x² + y² + z²  =  2 and the plane x + y - z  =  2 at the point (1,1,0).

Solution

  The tangent line to this curve lies on the tangent planes of each of the two surfaces.  We can conclude that this line is orthogonal to both normal vectors.  The gradient vectors are

        grad F  =  2x i + 2yj + 2z k        and        grad G  =  i + j - k

Evaluating these at the point (1,1,0) gives

        n₁  =  2 i + 2 j        and        n₁  =   i + j - k

The cross product is

       

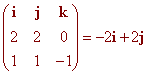
Now we use the formula for a line given a point and a parallel vector

        r(t)  =  i + j + t(-2i + 2j)

The parametric equations are 

        x(t)  =  1 - 2t        y(t)  =  1 + 2t        z(t)  =  0

PROBLEM 6  

If 

        a(t)  =  t i + j - k

find r(5) if 

        r(0)  =  i - k      and         r(1)  =  j + k
Solution:

We integrate to get the velocity function

        v(t)  =  (1/2 t² + v_x )i + (t + v_y )j + (-t + v_z )k

Integrate again to get 

        r(t)  =  (1/6 t³ + v_xt + r_x)i + (1/2 t² + v_yt + r_y)j + (-1/2t² + v_zt + r_z )k

Now plug in the first initial condition to get

        r_x i + r_y j + r_z k  =   i - k

So that 

        r_x  =  1        r_y  =  0        r_z  =  -1

Plugging these in and using the second initial condition gives

        (1/6 + v_x + 1)i + (1/2 + v_y)j + (-1/2 + v_z - 1)k  =   j + k  

So that 

        v_x  =  -7/6        v_y  =  1/2        v_z  =  5/2

Substituting gives

        r(t)  =  (1/6 t³ - 7/6 t + 1)i + (1/2 t² + 1/2 t)j + (-1/2t² + 5/2 t - 1)k

Now plug in 5 to get

        r(5)  =  (125/6  - 35/6 + 1)i + (25/2 + 5/2)j + (-25/2 + 25/2 - 1 )k

        =  16 i + 15 j - k