| Vector Fields Definition and Examples of Vector Fields We have now seen many types of functions. They are characterized by the domain and the range. Below is a list of some of the functions that we have encountered so far.
Example An important vector field that we have already encountered is the gradient vector field. Let f(x,y) be a differentiable function then the function that take a point (x0,y0) to gradf(x0,y0) is a vector field since the gradient of a function at a point is a vector. For example, if f(x,y) = 0.1xy - 0.2y then gradf(x,y) = 0.1yi + (0.1x - 0.2)j The sketch of the gradient is pictured below.  The best way to sketch a vector field is to use the help of a computer, however it is important to understand how they are sketched. For this example, we pick a point, say (1,2) and plug it into the vector field gradf(1,2) = .2i - .1j Next, sketch the vector that begins at (1,2) and ends at (1 + .2, .2 - .1). Notice that when we sketch vector fields, we use the definition that involves two points rather than the definition that assumes all vectors emanate from the origin. Example In physics, many vector fields satisfy the inverse square law. A vector field F satisfying the inverse square law has the property that if r = xi + yj + zj and u is the unit vector in the direction of r (u = r/||r||), then 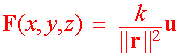 Examples of force fields that satisfy the inverse square law are gravitational force fields and electric force fields. Below is a plot of a vector field that satisfies the inverse square law. 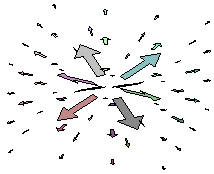 Notice that as the distance from the origin gets small, the vector become small quickly. For gravity, this tells us that as we fly away from the earth, we experience less gravity, until it seems like weightlessness. Other examples of vector fields that occur in nature include velocity fields. For example, the currents in the ocean ensure movement of the water. The if we sketch the velocity vector of at each point of the ocean, we get a vector field. A similar velocity field is produced from wind in the atmosphere. Conservative Vector Fields Our first and most important example was the gradient vector field. Can we go backwards? That is, given a vector field F, can we construct a function f with the property that F = gradf The answer to this question is only for some very special vector fields, which we call conservative.
F = is conservative, then So that M = fx and N = fy Now take partial derivatives with respect to y of the first equation and with respect to x of the second equation to get My = fxy and Nx = fyx Since mixed partial derivative are the same (for nice functions) we get My = Nx This turns out to be both a necessary and sufficient condition for a vector field to be conservative.
Example Determine which of the two vector fields are conservative A. F = 3xyi - x2j B. G = (1 + 2xy)i + (x2 - 2)j Solution For part A. we find My = 3x Nx = -2x Since they are not equal the vector field is not conservative. For part B. we find My = 2x Nx = 2x They are equal, so the vector field is conservative. Once we know that a vector field is conservative, how do we find the potential function? We investigate the relations M = fx and N = fy Example Find the potential function for the conservative vector field in the last example G = (1 + 2xy)i + (x2 - 2)j Solution We have M = 1 + 2xy = fx Integrating both sides with respect to x we get x + x2y + c(y) = f(x,y) Notice that the constant of integration may involve y terms since we are treating y as a constant. Now differentiate with respect to y to get x2 + c'(y) = fy = N = x2 - 2 Thus c'(y) = -2 Integrating with respect to y, we get c(y) = -2y We do not need a constant of integration here since we just want "a" potential function not the general potential function. Putting it all together, we get the potential function f(x,y) = x + x2y - 2y The Curl of a Vector Field If F is a vector field then we want to look at what operation we can do to it. One such operationis called the Curl of F. We define it as follows.
Notice that for a two dimensional vector field, where there is only a k component for a cross product, that if the curl is zero then the vector field field is conservative. Actually more is true. Remembering that all second order partial derivatives are independent of order for nice functions, we have
Example Determine if the vector field F = yz2i + (xz2 + 2)j + (2xyz - 1)k is conservative. If it is, find a potential function. Solution We calculate 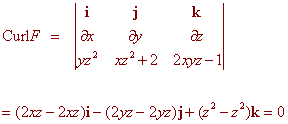 The vector field is conservative. Now equate fx = yz2 and integrate to get f = xyz2 + c(y,z) Notice the constant now depends on both y and z, since they were held constant when we integrated. Now take a partial with respect to y to get xz2 + cy(y,z) = fy = xz2 + 2 Hence cy(y,z) = 2 Integrate with respect to y to get c(y,z) = 2y + c(z) Notice that z is the only "constant" remaining. We get f = xyz2 + 2y + c(z) Now take a derivative with respect to z to get 2xyz + c'(z) = fz = 2xyz - 1 so that c'(z) = -1 finally integrate to get c(z) = -z The potential function is f(x,y,z) = xyz2 + 2y - z The Divergence of a Vector Field The curl of a vector field was defined as the cross product of the "dell" operator with the vector field. A curious student may try to take a dot product instead and see where it leads.
Notice that the curl of a vector field is a vector field, while the divergence of a vector field is a real valued function. Example Find the divergence of the vector field F = (x-3y)i + (x2z2 + cos(z3))j + (xyz2)k Solution We just take the three partial derivatives and add them up (1) + (0) + (2xyz) = 1 + 2xyz |
| |
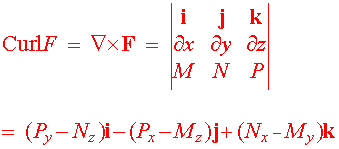
No comments:
Post a Comment