| Surface Integrals Surface Integrals for Parametric Surfaces In the last section, we learned how to find the surface area for parametric surfaces. We cut the region in the uv-plane into tiny rectangles and added up the area of the corresponding tiny parallelograms in the xy-plane. The area of these parallelograms was If we think of the surface as having varying density f(x,y,z), then the mass of this parallelogram will be and adding up all these masses and taking the limit as the rectangle sizes approach zero, gives the definition of the surface integral.
As with finding the surface area the integral typically results in an impossible integral. Example Find where S is the surface r(u,v) = ui + u2j + (u+ v)k 0 < u < 2 1 < v < 4 and f(x,y,z) = x + 2z Solution We find ru = i + (2u)j + k rv = k and take the cross product 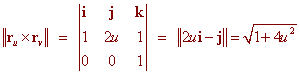 We have f(x(u,v),y(u,v),z(u,v)) = x(u,v) +2z(u,v) = u +2(u + v) = 3u + v We find Although this integral is possible, its solution is quite involved. You can verify that the surface integral evaluates to approximately 525.27. Surface Integrals for Surfaces that are Functions of Two Variables We have seen before that if z = g(x,y) is a surface such that g has continuous first order partial derivatives, then the parameterization r(u,v) = ui + vj + g(u,v)k has the property that This leads to the formula for surface integrals.
Example Find where S is the part of the paraboloid z = x2 + y2 that lies inside the cylinder x2 + y2 = 1 and f(x,y,z) = z Solution We have and f(x,y,z) = z = x2 + y2 At this point, you should be thinking, "This looks like a job for polar coordinates." And we get Let u = 1 + 4r2 du = 8r dr r2 = 1/4 u - 1/4 and the substitution gives us 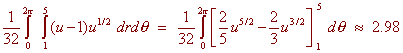 Oriented Surfaces and Flux we look to see if the region is on the right or left. Unfortunately, this definition does not work will for surfaces in three dimensions. The idea of right and left is not well defined. In fact not all surfaces can be oriented. We say that a surface is orientable if a unit normal vector can be defined on the surface such that it varies continuously over the surface. Below is an example of a non-orientable surface (called the Mobius Strip) 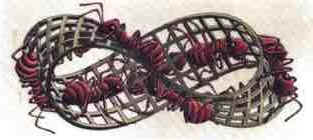 You can see that there is no front or back of this surface. Recall that a unit normal vector to a surface can be given by 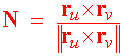 There is another choice for the normal vector to the surface, namely the vector in the opposite direction, -N. By this point, you may have noticed the similarity between the formulas for the unit normal vector and the surface integral. This idea leads us to the definition of the Flux Integral Consider a fluid flowing through a surface S. The Flux of the fluid across S measures the amount of fluid passing through the surface per unit time. If the fluid flow is represented by the vector field F, then for a small piece with area DS of the surface the flux will equal to DFlux = F . N DS Adding up all these together and taking a limit, we get
Notice that the denominator of N and the formula for dS both involve ||ru x rv||. Canceling, we get NdS = ru x rv dvdu for a surface that is defined by the function z = g(x,y), we get the nice formula NdS = -gx(x,y)i - gy(x,y)j + k (oriented upward) or NdS = gx(x,y)i + gy(x,y)j - k (oriented downward) Example Find the flux of F(x,y,z) = xi + 2yj + zk across the part of the surface z = x + y2 with upward pointing normal that lies within the box 0 < x < 3 2 < y < 5 Solution We compute NdS = -i - 2yj + k dydx and F . N dS = -x - 4y2 + x + y2 = -3y2 The flux integral is |
| |

No comments:
Post a Comment