| Double Integration in Polar Coordinates Many of the double integrals that we have encountered so far have involved circles or at least expressions with x2 + y2. When we see these expressions a bell should ring and we should shout, "Can't we use polar coordinates." The answer is, "Yes" but only with care. Recall that when we changed variables in single variable integration such as u = 2x, we needed to work out the stretching factor du = 2dx. The idea is similar with two variable integration. When we change to polar coordinates, there will also be a stretching factor. This is evident since the area of the "polar rectangle" is not just as one may expect . The picture is shown below. 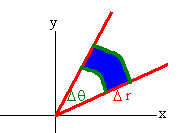 Even if Dr and Dq are very small the area is not the product (Dr)(Dq). This comes from the definition of radians. An arc that extends Dq radians a distance r out from the origin has length rDq. If both Dr and Dq are very small then the polar rectangle has area Area = r Dr Dq This leads us to the following theorem
Using Polar Coordinates Find the volume to the part of the paraboloid z = 9 - x2 - y2 that lies inside the cylinder x2 + y2 = 4 Solution The surfaces are shown below. 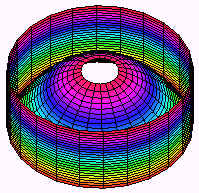 This is definitely a case for polar coordinates. The region R is the part of the xy-plane that is inside the cylinder. In polar coordinates, the cylinder has equation r2 = 4 Taking square roots and recalling that r is positive gives r = 2 The inside of the cylinder is thus the polar rectangle 0 < r < 2 0 < q < 2p The equation of the parabola becomes z = 9 - r2 We find the integral This integral is a matter of routine. It evaluates to 28p. Example Find the volume of the part of the sphere of radius 3 that is left after drilling a cylindrical hole of radius 2 through the center. Solution The picture is shown below 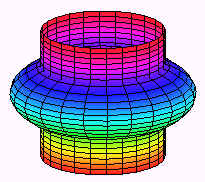 The region this time is the annulus (washer) between the circles r = 2 and r = 3 as shown below. 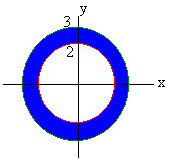 The sphere has equation x2 + y2 + z2 = 9 In polar coordinates this reduces to r2 + z2 = 9 Solving for z by subtracting r2 and taking a square root we get top and bottom surfaces of We get the double integral This integral can be solved by letting u = 9 - r2 du = -2rdr After substituting we get 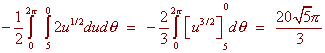 |
MANIC FM
Saturday, July 24, 2010
Vectors Calaulus 1.20
Subscribe to:
Post Comments (Atom)
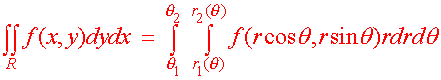
No comments:
Post a Comment