Line Integrals Definition of a Line Integral By this time you should be used to the construction of an integral. We break geometrical figure into tiny pieces, multiply the size of the piece by the function value on that piece and add up all the products. For one variable integration the geometrical figure is a line segment, for double integration the figure is a region, and for triple integration the figure is a solid. The geometrical figure of the day will be a curve. If we have a function defined on a curve we can break up the curve into tiny line segments, multiply the length of the line segments by thefunction value on the segment and add up all the products. As always, we will take a limit as the length of the line segments approaches zero. This new quantity is called the line integraland can be defined in two, three, or higher dimensions. Suppose that a wire has as density f(x,y,z) at the point (x,y,z) on the wire. Then the line integral will equal the total mass of the wire. Below is the definition in symbols.
Evaluating Line Integrals This definition is not very useful by itself for finding exact line integrals. If data is provided, then we can use it as a guide for an approximate answer. Fortunately, there is an easier way to find the line integral when the curve is given parametrically or as a vector valued function. We will explain how this is done for curves in R2. The case for R3 is similar. Let r(t) = x(t)i + y(t)j be a differentiable vector valued function. Then We are now ready to state the theorem that shows us how to compute a line integral.
Example Find the line integral where C is the ellipse r(t) = (2cos t)i + (3sin t)j 0 < t < 2p You may use a calculator or computer to evaluate the final integral. Solution We find We have the integral With the help of a machine, we get 15.87 The main application of line integrals is finding the work done on an object in a force field. If an object is moving along a curve through a force field F, then we can calculate the total work done by the force field by cutting the curve up into tiny pieces. The work done W along each piece will be approximately equal to dW = F . Tds Now recall that r'(t) T = ||r'(t)|| and that ds = ||r'(t)||dt Hence dW = F . r'(t) dt As usual, we add up all the small pieces of work and take the limit as the pieces get small to end up with an integral.
Example Find the work done by the vector field F(x,y,z) = xi + 3xyj - (x + z)k on a particle moving along the line segment that goes from (1,4,2) to (0,5,1) Solution We first have to parameterize the curve. We have r(t) = <1,4,2> + [<0,5,1> - <1,4,2>]t = <1 - t, 4 + t, 2 - t> and r'(t) = -i + j - k Taking the dot product, we get F . r'(t) = -x + 3xy + x + z = 3xy + z = 3(1 - t)(4 + t) + (2 - t) = -3t2 -10t + 14 Now we just integrate Notice that work done by a force field on an object moving along a curve depends on the direction that the object goes. In fact the opposite direction will produce the negative of the work done in the original direction. This is clear from the fact that everything is the same except the order which we write a and b. Line Integrals in Differential Form We can rewrite r'(t)dt as dr dx dy dz dt dt dt dt = dx i + dyj + dzk So that if F = Mi + Nj + Pk then F . r'(t)dt = Mdx + Ndy + Pdz This is called the differential form. Example Find where C is the part of the helix r(t) = sin t i + cos t j + t k 0 < t < 2p Solution We have r'(t) = cos t i - sin t j + k so that ydx + zdy = (cos2t - t sin t)dt This leads us to the integral with a little bit of effort (using integration by parts) we get 3p |
MANIC FM
Saturday, July 24, 2010
Vectors Calaulus 1.28
Subscribe to:
Post Comments (Atom)
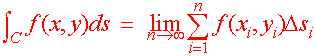
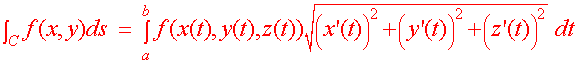
No comments:
Post a Comment