Vectors Calaulus 1.29

Conservative Vector Fields and  Independence of Path The Fundamental Theorem of Line Integrals Consider the force field representing the wind shown below 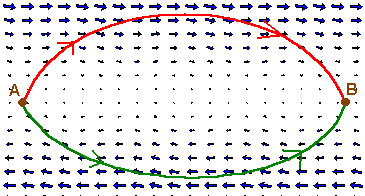        You are a pilot attempting to minimize the work your engines need to do.   Does it matter which path you take?  Clearly the red path goes with the wind and the green path goes against the wind.  With this vector field, work is dependent on the path  that is taken.   Next consider the vector field          F(x,y)  =  yi + xj shown below         It turns out that going from point A to point B, every path leads to the same amount of work done.  What is special about this vector field?   The key here, as you can quickly check, is that the vector field F is conservative. (My  =  Nx ).  Since for a conservative vector field, all paths produce the same amount of work, we seek a formula that gives this work quantity. The theorem below shows us how to find this quantity.  Notice the strong resemblance to the fundamental theorem of calculus. The Fundamental Theorem of Line Integrals Let F be a conservative vector field with potential function f, and C be any smooth curve starting at the point A and ending at the point B.  Then                The next example demonstrates the power of this theorem. Example Find the work done by the vector field          F(x,y)  =  (2x -3y)i + (3y2 - 3x)j         along the curve indicated in the graph below 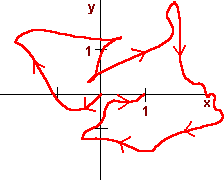        Solution First notice that          My  =  -3  =  Nx We can use the fundamental theorem of line integrals to solve this.  There are two approaches.   Approach 1 We find the potential function.  We have          fx  =  2x - 3y Integrating we get         f(x,y)  =  x2 - 3xy + c(y) Now take the derivative with respect to y to get         fy  =  -3x + c'(y)  =  3y2 - 3x  Hence          c'(y)  =  3y2 and          c(y)  =  y3  The potential function is          f(x,y)  =  x2 - 3xy + y3  Now use the fundamental theorem of line integrals to get         f(B) - f(A)  =  f(1,0) - f(0,0)  =  1 Approach 2 We since the vector field is conservative any path from point A to point B will produce the same work.  Hence the work over the easier line segment from (0,0) to (1,0) will also give the correct answer.  We parameterize by          r(t)  =  ti          0  <  t  <  1 we have         ri(t)  =  i        so that         F . dr  =  ((2x -3y)i + (3y2 - 3x)j) . i  =  2x - 3y  =  2t Now just integrate                  Proof of the Fundamental Theorem of  Line Integrals To prove the fundamental theorem of line integrals we will use the following outcome of the  chain rule: If          r(t)  =  x(t)i + y(t)j  is a vector valued function, then          d/dt f(r(t))  =  fx x'(t) + fy y'(t) We are now ready to prove the theorem.  We have 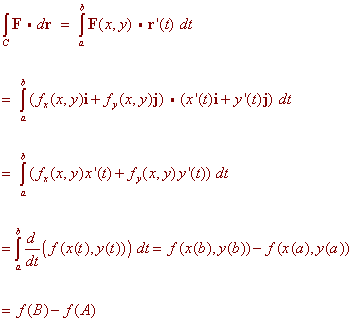        Independence of Path and Closed Curves Example Find the work done by the vector field           F(x,y)  =  (cos x + y)i + (x+ esin y)j + (sin(cos z))k along the closed curve shown below 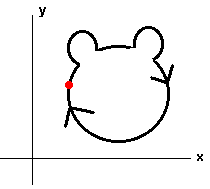        Solution First we check that F is conservative.  We have 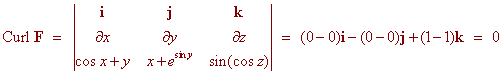             Since the vector field is conservative, we can use the fundamental theorem  of line integrals.  Notice that the curve begins and ends at the same place.  We do not  even need to find the potential function, since whatever it is, say f, we have         f(A) - f(A)  =  0 In general, the work done by a conservative vector field is zero along any closed curve.  The converse is also true, which we state without proof. Theorem:  Conservative Vector Fields and Closed Curves Let F be a vector field with components that have continuous first order partial derivatives and let C be a piecewise smooth curve.  Then the following three statements are equivalent 1.  F is conservative. 2.    is independent of path. 3.    for all closed curves C.