| Iterated Integrals and Area Just as we can take partial derivative by considering only one of the variables a true variable and holding the rest of the variables constant, we can take a "partial integral". We indicate which is the true variable by writing "dx", "dy", etc. Also as with partial derivatives, we can take two "partial integrals" taking one variable at a time. In practice, we will either take x firs t then y or y first then x. We call this an iterated integral or a double integral.
Example Find the double integral of f(x,y) = 6x2 + 2y over R where R is the region between y = x2 and y = 4. Solution First we have that the inside limits of integration are x2 and 4. The region is bounded from the left by x = -2 and from the right by x = 2 as indicated by the picture below. 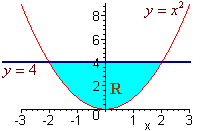 We now integrate 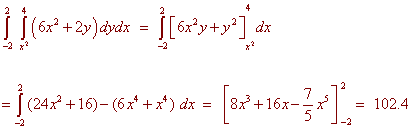 Changing the Order of Integration If a region is bounded from the left by x = h1(y) and the right by x = h2(y) and below andabove by y = c and y = d, then we can find the double integral of "dxdy" by first integrating with respect to x then with respect to y. Sometimes there is a choice to make as to whether to integrate first with respect to x and then with respect to y. We do whatever is easier. Example Find the double integral of f(x,y) = 3y over the triangle with vertices (-1,1), (0,0), and (1,1). 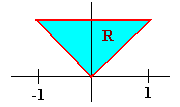 Solution If we try to integrate with respect y first, we will have to cut the region into two pieces and perform two iterated integrals. Instead we integrate with respect to x first. The region is bounded on the left and the right by x = -y and x = y. The lowest the region gets is y = 0 and the highest is y = 1. The integral is 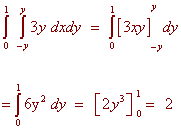 Example Evaluate the integral 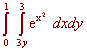 Solution Try as you may, you will not find an antiderivative of 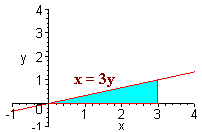 We can switch the order of integration. The region is bounded above and below by y = 1/3 x and y = 0. The double integral with respect to y first and then with respect to x is The integrand is just a constant with respect to y so we get 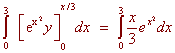 This integral can be performed with simple u-substitution. u = x2 du = 2x dx and the integral becomes 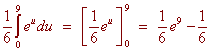 Recall from first year calculus, if a region R is bounded below by y = g1(x) and above by y = g2(x), and a < x < b, the area is given by There is another way of achieving this expression. If we let the integrand by 1 then the double integral over the region R is 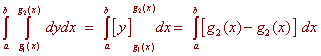 This gives us another way of finding area.
then the double integral of 1 dxdy can also be used to find the area. Example Set up the double integral that gives the area between y = x2 and y = x3. Then use a computer or calculator to evaluate this integral. Solution The picture below shows the region 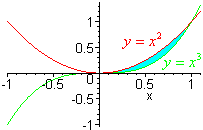 We set up the integral 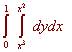 A computer gives the answer of 1/12. |
MANIC FM
Saturday, July 24, 2010
Vectors Calaulus 1.18
Subscribe to:
Post Comments (Atom)
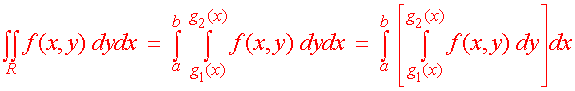
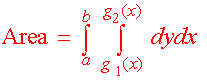
No comments:
Post a Comment